AtCoderで水色になりました
緑の色変記事を書いてから早くも3ヶ月ほどが経ちましたが……ABC168にて、無事水色Coderになりました!!
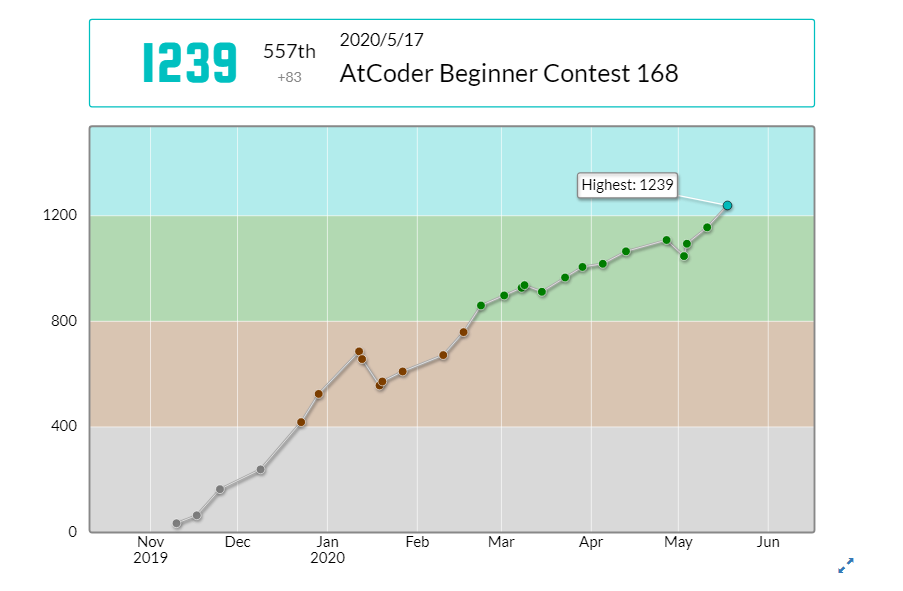
順位は557位で、パフォーマンスは1781でした!これが初めての青perfです。

さて色変記事なので「水色になるまでやったこと」的なのを書きたいのですが……やったことと言えばコンテストに出て、復習して、たまに水diffを解くくらいのものなのであまり参考にならない気がしています、申し訳のなさ(AtCoderではまだ440問くらいしかAC出してません)
最近はApexかMinecraftしかしていません、FAKEだろ
ただ言えることは、やっぱりコンテストに出るのって最大の精進だと思うのでCodeforcesとかでコンテストに出まくるといいと思います。AtCoderと必ずしも問題傾向が等しいわけではないので、AtCoderのレーティングに直結することは保証しかねますが、逆に言うとAtCoderでレートが上の人に勝つチャンスがあります。
何もAtCoderだけが競プロでは無いので、競プロが好きな人こそCodeforcesはおすすめです。ある程度英語が読めれば十分なので。どうしても無理ならDeepLを使いましょう。
あとE8さんのこちらの精選100問はとてもおすすめです。既に読んで取り組んでいる方も多いと思います。
まだ半分も終わっていないので自分も青になるために解いていきたいと思います……。
最後になりますが、vtuberにハマると競プロとの相性が悪すぎる(精進時間の確保的な意味で)ので気をつけたほうがいいです、はい。趣味が基本競プロと相性悪くて泣ける。(最近は追加で学業が競プロを侵食しています)
ちなみに私はホロライブ推しです。
【ホロライブ】だいたい清楚なデビュー初期と現在の配信を比較してみた【ホロろぐ001】
高校卒業までに青目指して頑張りたいと思います。
競プロで悩んだ計算量の話
競プロの精進をしていて、個人的に悩んだことがあったので書いておきます。
誰かの助けになれば、と思います。
※各問題の解法ネタバレ有り
ABC097 C - K-th Substring
問題概要:
文字列 が与えられる。
の部分文字列のうち、辞書順で
番目に小さいものを出力せよ。
()
※ とします
基本方針としては、制約が小さいのでC++ならsetにでも突っ込んで順番に取り出せばよいです。setはデフォルトでソートされた状態で保持してくれますからね。
というわけで一番最初に提出したコードがこちら。
Submission #11947075 - AtCoder Beginner Contest 097
うん、ループは だしsetへのinsertは対数オーダーだから通るはず……って言ってると、なぜかTLEに。さて、なぜでしょうか。
強い人に質問してみると、これ実は になってるらしいとのこと。
どこで が発生しているかというと、文字列の比較でした。
文字列の比較なんてどこでした?という感じなのですが、よく考えてみるとsetへinsertするときに毎回発生しています。ソートされた状態で要素を保持するためには比較をしなければなりませんからね……。これが盲点でした。
ソートをする際、比較そのものの回数は なわけですが、その比較1回あたりに
かかっていたわけです。(正確には比較する文字列の長さのmin?)
そんなわけで、もうちょい計算量を削らなければなりませんが、この問題の場合には の制約が小さいおかげで、長さ6以上の部分文字列はsetへinsertしないことによりTLEを回避できました。
ACコード(1行追加しただけ):
Submission #11947828 - AtCoder Beginner Contest 097
ABC162 E - Sum of gcd of Tuples (Hard)
問題概要:
以上
以下の整数からなる長さ
の数列の全てについてgcdを求め、その和を計算せよ。
()
基本方針は公式解説の通りで、 に対して最大公約数が
となるような数列の数を求めてその和を求めます。
こちらが書いたコード。
Submission #11975132 - AtCoder Beginner Contest 162
注目してほしいのは、もちろんループの部分。
for (int x = k; x > 0; x--) {
lint t = k / x;
t = modpow(t, n);
lint x2 = x + x;
while (x2 <= k) {
t -= c[x2];
x2 += x;
}
t = ((t % MOD) + MOD) % MOD;
c[x] = t;
res += t * x;
res %= MOD;
}
内側のwhileで、倍数の分の数を引いています。
ここで気になるのが、このwhileループ、計算量はどうなるの?ということです。
ACを出したときはよく分かっていないまま通ってしまったのですが、別にTLEとなってもおかしくなかったと思います。
ここで今一度、ループの実行回数を考えてみます。
whileループの回数は、コード中の変数 の値に依存しています。具体的には、
の倍数の個数の分だけ、ループが実行されるはずです。
ということは、 のときは
回、
のときは
回、…という風になるので(本当は小数点以下切り捨てですがあえてこう書きます)、全体でのループの回数は以下の和になるはずです。
もうこう書いてしまったら分かりやすいのですが、これを でくくります。
そうすると、こうです。
右の分数の和は第 調和数
なので、これは
に近似することが出来て、最終的な計算量は
ということになります。
コンテスト中にここまで思考を詰めれる人、すごいな……。
AtCoderで緑になりました
茶Coderになってから二ヶ月経ち、ようやく緑Coderになりました!

一度レートが下がりまくったときはどうなることかと思いましたが、その後は特に何事もなくレート上がりました。よかった……。(下がったのはドワンゴコンで水パフォが出てしまって無駄にレートが伸びてしまった説が濃い)
緑色というと、「エンジニアとしてもある程度の安心感」とのこと(chokudaiさん談)なので、自尊心高まりますね。Unityとかソフトウェア開発もやらないとなあ
さて色変したからには「緑色になるまでにやったこと」みたいなのをまとめてみようかなと。水色になるまで、とかよりは有用性低い感じはしますが、競プロはじめてすぐの人へのTipsになるといいなと思います。
まず、どのコンテストに出たらいいの?という話。
AtCoder上でのコンテストは、ABC級、ARC級、AGC級(+unratedのやつ)に分類分けされています。コンテストの名前の左に付いている丸の色です。青ならABC級、橙はARC級、赤はAGC級ですね。
AtCoderのレーティングシステムには、コンテストの参加回数が少ないうちはパフォーマンスよりレーティングが大分低くつくような仕組みがあります。これがあるので、レートを上げようとするならコンテストにたくさん出ておこう、となるのですが、ここでARC級とかAGC級にも出るべきなのか?という疑問が浮かぶと思います。
この質問への個人的な解答は、「No」です。出たほうがいいよ、という人もいるんですけどね。
私がこう思う理由ですが、ARC級とかAGC級とかに出てもあまり問題が解けないからです。結局1完とかになってしまうんですよね。そうすると、あまりパフォーマンスが出なかったりして、レートもあまり伸びない。ひどいと下がったりしちゃいます。
そうなると問題になるのが、自分の競プロのモチベ維持です。やっぱり、競プロが楽しくてもレートが伸び悩んだりするとあまりいい気分にならないと思いますし、急にARCとかに参加して問題が解けなかったから「自分は競プロに向いてないのかな……」みたいに悩んじゃうとか、そういう人も居るんじゃないかなと思ったりします。
別にARC級とかAGC級の問題が最初解けないのなんて当然で、私も700点問題とか自力で解けないし、ちょっとずつ解けるようになっていくものだと思います。
やっぱり競プロ始めてすぐは成功経験の方が継続の糧になるので、無理に上級のコンテストに出なくてもいいんじゃないかな、と思うわけです。
(なんか書いてたら長くなってしまったな…)
あとは、緑までに知っておくべきアルゴリズムの話です。
パッと使えるようにしておくべきものは、こんな感じ。
(・C++のSTL、queueとstack、map、setとか)
・素因数分解、GCD、LCM
・mod p逆元、二項係数(nCr)、二分累乗法、二分乗法(正しい名前なのか不明)
・二分探索
・貪欲法
・一次元DP、典型的な桁DP
・DFS、BFS
・しゃくとり法
・累積和、(imos法)
逆に今まで使う緑diff問題に出会ったことがないアルゴリズム
・UnionFind木、セグ木、BIT
・最小全域木(クラスカル法)
・ベルマンフォード法、ダイクストラ法
ベルマンフォードとダイクストラは、緑で出てもおかしくない気はしますが、まあとりあえずこんな感じで。
最後にですが、やっぱり精進は毎日続けといたほうがいいです。緑くらいまでだと、まだたまにこのアルゴリズム知らなかったから解けなかった!みたいな事態が発生するので、過去問で演習量積んでおくのはアドバンテージになると思います。解説までしっかり読んだり動画見たりしましょう。
というわけで、以上です。高校卒業までに青になることを目標に頑張っていきます。
円周率の近似値 ~ ゼータ関数の特殊値
寝る前にちょっとメモ書きです.
であるから、
ここで、0909が繰り返されている部分に注目して、それより前の と合わせてそれぞれ分数化する.
\begin{align}
97.4 &= 97 + \frac{4}{10} \\
\frac{9}{990} &= 0.0090909 \ldots
\end{align}
したがって、
\begin{align}
97 + \frac{4}{10} + \frac{9}{990} = \frac{2143}{22} = 97.4090909 \ldots
\end{align}
よって、円周率は以下のように近似できる。
\begin{align}
\pi \approx \sqrt[4]{\frac{2143}{22}}
\end{align}
x^2 = 2^x ~ ランベルトのW関数と共に
お久しぶりです。久しぶりに数学の話でもしようかなと思います。
\begin{align}
x^2 = 2^x \quad (x \in \mathbb{R})
\end{align}
今回はこの方程式について、取り扱います。
突然ですがみなさん、この方程式解けますか?
……「甘く見てもらっちゃ困る、2と4だろ?」ときっと多くの人が感じているでしょう。もちろん、その2つも解になりますね。代入してみれば自明です。
ここで、ちょっとグラフを観察してみることにしまよう。
上の方程式は、2つの関数 と
の交点を求めることと同値なので、とりあえずグラフを描いてみます。

うーん、確かに のところでしっかりグラフが交わっていますね。
「なんでそんな中途半端な画像の切り抜き方なんだ」、って? 気になります?しょうがないですね~。
真の全体像は、こちら。

さっきと何が違うのって、……うん?

な、なんかあった!!!
……という感じで、実は上の方程式には、負の実数解がもう1つ存在するのです。
この値は、一体どんな数なのか? 今回はこれを探っていきたいと思います。
方程式を解くだけの簡単なお仕事
あんまり簡単じゃない。
とりあえず、元の式を変形していってみましょう。
\begin{align}
x^2 = 2^x
\end{align}
元の方程式はこれでした。とりあえず、指数絡んでるので両辺自然対数を取りましょう。「2を底にしたほうがいいんじゃない?」とかあるかもしれませんが、後でその理由は分かります。
\begin{align}
2 \log |x| = x \log 2
\end{align}
対数取っただけですね。ここで、ちょっと式の整理をします。
\begin{align}
x^{-1} \log |x| = \frac{1}{2} \log 2
\end{align}
さて、一見してここから について解くのは果たして可能なのか?と思えます。
ここで本日の強力な武器の登場です。それが、ランベルトのW関数です。
\begin{align}
z = W(z) e^{W(z)}
\end{align}
上のような式を満たす関数 がランベルトのW関数です、といってもいまいちしっくりこないと思います。
この関数は、関数 の逆関数
となっています。
つまり、 が成り立つということです。これだけ分かれば十分です。
これを使って、さらに式変形していきます。
絶対値が式の中にあるので、場合分けしましょう( のときは明らかに解にならないので除外です)。
まず が正の場合。
\begin{align}
x^{-1} \log x = \log \sqrt{2}
\end{align}
普通にそのまま絶対値を外しました。あと は対数の中に入れてしまいます。
さらに、W関数が使える形に持っていきます。
\begin{align}
\log x \, e^{- \log x} = \log \sqrt{2}
\end{align}
両辺-1倍してあげれば、
\begin{align}
- \log x \, e^{- \log x} = - \log \sqrt{2}
\end{align}
になって、左辺が の形になりました。
ここで両辺にW関数を使います。
\begin{align}
W(- \log x \, e^{- \log x}) &= W(- \log \sqrt{2}) \\
- \log x &= W(- \log \sqrt{2})
\end{align}
したがって、 について解くと、
\begin{align}
x = e^{-W(- \log \sqrt{2})}
\end{align}
となります。
さて、 は正という仮定だったので、これは2と4に一致するはずですが……1個しか解が無いですね?
実は、このランベルトのW関数は多価関数、という奴でちょっと厄介な性質があるのです。ざっくり言うと、同じ入力値から出力の値が複数出てきてしまいます。
詳しい話をすると、この関数は開区間 上で二価となります。上で出てきた
という値はギリギリこの中に収まっていて*1、従って2と4という2つの値を取ることになるのですね。
これと同様に、 が負の場合の解も求めましょう。
流れとしてはほぼ同じです。W関数が使えるように変形します。
\begin{align}
x^{-1} \log (-x) = \log \sqrt{2}
\end{align}
ちょっとトリッキーに、以下のようにします。
\begin{align}
(-x)^{-1} \log (-x) = - \log \sqrt{2}
\end{align}
あとはさっきと同じです。
\begin{align}
- \log (-x) \, e^{- \log (-x)} = \log \sqrt{2}
\end{align}
符号をお間違えなきよう。
\begin{align}
W(- \log (-x) \, e^{- \log (-x)}) &= W(\log \sqrt{2}) \\
- \log (-x) &= W(\log \sqrt{2})
\end{align}
ゴールが見えましたね。
\begin{align}
x = -e^{-W(\log \sqrt{2})}
\end{align}
eの前にマイナス符号が付いてるので、しっかり負の値であることがわかります。
さてこの具体的な値を求めたいのですが、実は残念ながらこの値は2や4のように綺麗にはなりません。しかも超越数になります。
\begin{align}
x = -e^{-W(\log \sqrt{2})} = -0.766664695962123 \dots
\end{align}
ちなみにこの範囲ではW関数は一価なので、負の解はこれだけです。
\begin{align}
(-0.766664695962123 \dots)^2 = 2^{-0.766664695962123 \dots}
\end{align}
以上、明日から使える豆知識でした。
週末のコンテストの反省をする
ABC151で500台とかいうパフォーマンスを叩き出して割と心が折れたので精進と備忘録ついでに最近解いた問題のまとめを書きます。
第6回 ドワンゴからの挑戦状 予選 B - Fusing Slimes(600点)
解法とか方針とかは解説pdfと動画参照。
使うアルゴリズムについて。有限素体 における調和数的なものを計算する必要がありますので、それはつまりある自然数に対してその逆元を計算しなければならないということです。
逆元の計算については詳しくは上の記事に書かれていますが、Fermatの小定理を使うのが理解するのにも手っ取り早くてよいです。
法が であるとき、自然数
の逆元は
なので、愚直に計算すると計算量が
となってしまいますが、これも上の記事に書かれている二分累乗法によって、対数オーダーに落とすことができます。
Submission #9493452 - Dwango Programming Contest 6th
ABC 151 F - Enclose All(600点)
最小包含円というやつです。典型どころか超有名とのこと(すぬけさん談)。
解説できないので下のサイトからソースをコピペして提出しましょう。
Spaghetti Source - 最小包含球 (move-to-front heuristics)
Submission #9489664 - AtCoder Beginner Contest 151
ABC 151 D - Maze Master(400点)
方針については、BFSだろうと秒で分かると思います。
ゴール地点を定めずにBFSすると、各地点までの最短距離が分かるというやつです。
迷路上の全ての点をそれぞれスタート地点に定めて最も遠い距離を記録、そして最後にそれらのmaxを通ればACです。
ちなみに私は本番中に変数名の i と j を間違えてるのに最後まで気づかず400点を逃しました。辛い。
Submission #9489255 - AtCoder Beginner Contest 151
ABC 151 A - Next Alphabet(100点)
わずか3ByteでACを出せると話題の問題です。完全に余談ですね。
Brainf***を使うと、3文字で書けます。
ソースコードは、「,+.」です。
Submission #9489181 - AtCoder Beginner Contest 151
ABC 150 C - Count Order(300点)
C++限定解法ですが、next_permutation()を使うと書くだけでACできます(Pythonでも順列生成する関数はあるらしい)。
上手いことに辞書順で生成してくれるので、カウンタで何番目かだけ記録してあげれば良いです。
Submission #9391152 - AtCoder Beginner Contest 150
反省
・焦りすぎない。問題をちゃんと読むこと。早解きよりも大事。
・コードのツギハギはあんまよろしくない。多分現場猫並にコードはちゃんと確認したほうがいい。
最近解いた問題の解説をしてみる(AtCoder)
タイトル通りです。editorial読んだほうがええやろという感想は尤もなのですが、自分の理解のために書いておこうかと思います。(解説と違う解答だったりしたので)
ABC057 C - Digits in Multiplication(300点)
問題文の要約をするまででもないですね。
方針としては、普通に積が となるような2つの整数の組を全探索していけばいいです。注意として、
から順に
の約数となっているかチェックするわけですが、チェックする最大の整数は
とすれば十分です。割る数を
とすれば、
より大きい約数は
として既に出てきているので、ここで計算量を落とせます。全体の計算量は
となり、今回の制約では十分余裕を持って間に合います。
桁数の計算は普通に各言語に実装されているであろう常用対数を使えばいいと思います。常用対数の値に1を加えたものが整数の桁数になるので、これで計算できます。
Submission #9320273 - AtCoder Beginner Contest 057
(自分の提出)
ABC142 D - Disjoint Set of Common Divisors(400点)
解答では最大公約数を使った簡潔なもの等がありましたが、普通にこの問題も上の問題と同じ発想(ほぼ実装も同じ)で解けます。
まず方針ですが、少し考えれば選ぶことのできる正の公約数というのは、1か素数であるものしかありえないことが分かります。
これが分かれば、さっきと似たようなことで公約数を全て配列にでも突っ込んで全て素数判定してしまえばいいです。
公約数の計算は なので、これも余裕をもって間に合います。
実装上の注意としては、C++のstd::vector等を使うと入力が平方数のとき折返し地点で同じ約数を2回カウントしてしまうので気をつけましょう。std::set等を使えば問題ないです。
Submission #9320526 - AtCoder Beginner Contest 142
ARC033 B - メタ構文変数(?点)
配点が40と70に分かれてるらしいですが自分の提出についてる点数は100点なの謎です
要約:
与えられた数の集合 の共通部分と和集合の要素数の比を求めよ。
方針ですが、和集合については普通にsetにでも値をinsertしていって最後にsize()で出力すればいいです。共通部分は、どちらかの集合の要素全てについて、もう一方の集合にも含まれているかどうか調べればよいです(std::setを使うならfind()を使えば簡単です)。特に難しいことは無い。
Submission #9332944 - AtCoder Regular Contest 033
第二回全国統一プログラミング王決定戦予選 B - Counting of Trees
頂点 をrootとする木を考えます。
まず前提として であってかつそれ以外は0でない必要があります。そうでなければ答えは0です。
距離0の頂点には距離1の頂点から辺が伸びていて、距離1の頂点には距離2の頂点から辺が伸びていて……という風になっているので、まずはそれぞれ距離0、1、2、…となっているような頂点の数を数えましょう。このときに、距離1と距離3の頂点は存在するけど距離2の頂点は無い、のような状態になるとこれも木を構成できないので、答えは0です。
実装していく際には、数列 をソートしておくといいです。
あとは先頭からしゃくとり法しましょう。
ここまで来たら、あとは頂点から辺の伸ばし方が何通りあるか数えればいいです。
例えば、距離1の頂点が2つあり、距離2の頂点が3つ存在するとき、その繋げ方は 通りになります。距離
の頂点それぞれについて、距離
の頂点のどれを選ぶか、という話なのでこのような計算になります。
ここは解説動画見たほうがいいです。
頭の悪い数え方をしたりするとTLEになるので気をつけましょう(実話)。