sin(x)/xの極限を矛盾なく証明してみる

お久しぶりです。書き残しておきたいネタができたので、書くことにしました。

さて、以下のような定理があります。

\begin{align}
\lim_{x \to 0} \frac{\sin(x)}{x} = 1 \tag{1}
\end{align}

数学において、最も有名な極限問題と言ってもいいと思います。読者のみなさんも、よく知っていることと思います。

なぜこんなにも知られているかと言えば、まず高校数学において登場するからでしょう。理系の方ならば、必ず通る道です。三角関数を微分するのにこの定理が必要になるので、その前に習うことになっていると思います。

教科書の極限の演習問題は、そのほとんどがあまり深い意味の無い演習用のものですが、この定理に関してはそういった出題背景なり、意義があるわけですね。

どのように証明をするか

ところで今回注目したいのは、この定理の証明手法です。
みなさんは、どのように習いましたでしょうか。

一番よくあるタイプが、幾何的に面積を用いて(1)の左辺を上下から評価する証明です。

manabitimes.jp

高校数学の美しい物語さんの、こちらの記事にそのまま証明が記されています。
（以下、こちらの図を見ながら話をします）

しかしながら、一見正しいように思われるこの証明手法、時折「循環論法である」と言われたりします。さて、どこが怪しいのでしょうか。

何が矛盾しているのか

上記の証明において得られた、 < < という関係式は正しく成立しているものです。

問題となるのは、それを得る過程の方ですね。

この証明では、不等式を得るために三角形と扇形の面積の比較を行いました。では、面積の比較が間違っていたか？というと、そうではないですね。これら3つの図形の大小関係自体は、図より明らかなものとして良いでしょう。

この証明で怪しいポイントは、「それぞれの図形の面積ってどうやって計算されているの？」というところです。
三角形の面積は流石に認めてもよいと思いますが（四角形を半分にしただけですから）、扇形の面積はそれと比べて少し複雑です。

扇形の面積をどのように計算するかを思い出してみましょう。
まず、扇形は円の一部ですから、円の面積が必要ですね。

では、円の面積はどのように計算されているでしょうか。曲線に囲まれた部分の面積ですから、一般には積分で求めることになります。

実際に計算してみましょう。2次元の座標平面上の円を考えます。

円の面積をとすると、

\begin{align}
S = 4 \int_0^r \sqrt{r^2-x^2} dx
\end{align}

と書くことができます。と置換すると、となるので、

\begin{align}
4 \int_0^r \sqrt{r^2-x^2} dx = 4r^2 \int_0^{\frac{\pi}{2}} \cos^2 \theta d\theta
\end{align}

が得られます。ここで半角の公式を用いれば、

\begin{align}
4r^2 \int_0^{\frac{\pi}{2}} \cos^2 \theta d\theta &= 2r^2 \int_0^{\frac{\pi}{2}} \left( 1 + \cos 2\theta \right) d\theta \\
&= 2r^2 \left[ \theta + \frac{1}{2} \sin 2\theta \right]_0^{\frac{\pi}{2}} \\
&= \pi r^2
\end{align}

となり、が示せました。

さて、以上のように円の面積を計算しましたが、主に2つの道具を用いました。三角関数の微分と加法定理です。

……ん？微分？

そういうわけで、三角関数の微分には(1)の定理が必要なのに、その証明に三角関数の微分を用いているため循環論法である、と言われることがあります*1。

しかしながら、この指摘はどうやら誤りのようです。この記事を書くのにいくつか参考文献を読んでみましたが、円の面積は三角関数の微分という過程を踏むこと無く計算できる（らしい）*2ので、先程の証明は矛盾していないというのが一般論とされているみたいです。

とはいえ、この証明に文句が付くことがあるのも事実なので、今回の記事ではこれを回避して(1)の定理に別の証明を与えたいと思います。

面積を使うのをやめよう

先程の証明で何が怪しいかと言えば円の面積を使ったことなので、これを何かで代替できないか考えてみます。

（回避方法として、三角関数をMaclaurin級数により定義したり、微分方程式により定義したりすることもできますが、話が面白くなくなるのでここではこれは禁止としましょう）

面積じゃなくて、弧の長さを使ってみたらどうでしょうか。弧長の比較ならば、証明のアウトラインもそんなに大きく変わらずに済みそうです。

この証明方法も割とよくある手法で、以下のようなものです。

図1

であるとします。

図において、線分AH < 弦AB < 弧AB < 線分CBという不等式が成立します。

線分AHは、弧ABは弧度法の定義より、線分CBはですので、すなわち

\begin{align}
\sin x < x < \tan x
\end{align}

が得られます。

これ以降は、面積を用いた証明と同様にして、(1)を示すことができます。

それは本当に自明ですか？

さて、矛盾を回避して証明ができました。と言いたいところですが。
上の証明は、実はかなり怪しいです。注意深い人や、数学に慣れている人ならば、「ん？」と思った箇所があるかもしれません。

しかも、インターネット上で循環論法を回避した証明として掲載されているのが、大抵この証明だったりするので、証明を書くのに参考にしようとしている人は注意しておいたほうが良いでしょう。

では、何が危ないのか。まあ一箇所しか無いんですが……。

上の証明において、「線分AH < 弦AB < 弧AB < 線分CB」という不等式を利用しました。この式をもう少し落ち着いて観察してみます。

下から評価を与える「線分AH < 弦AB < 弧AB」の方。これは確かに図から明らかとしても良さそうです。
しかし、一方で上から評価をしている部分である「弧AB < 線分CB」。これは本当に自明でしょうか？本当に弧ABより線分CBの方が長いと言えるでしょうか？

まあ、ネタバレしてしまうと「弧AB < 線分CB」という不等式自体は厳密に成立しているものなのですが、この不等式を証明で使いたいのならばもう少し長い話が必要になるでしょう（意外とこの不等式、示そうとすると面倒です）。

じゃあどう解決するかと言うと、上からの評価に線分CBを使うのをやめ、線分HA+線分HBを使うことにします。

曲線の長さの定義

本編の証明に入る前に、曲線の長さを扱うことになるのでこの話を先にしておきます。

ja.wikipedia.org

基本はこちらのWikipediaの定義の項を読んでいただければよいです。

説明を読んだだけだと分かりづらいと思いますので、弧ABの長さを例にとってみます。

まず、先程の証明の図に座標を入れておきます。2次元座標系の単位円だとすると、ベクトルを用いて、と書けます。

次に、BからAまでの円周上の分点をとし、各点の座標をと書くことにします。

このとき弧ABの長さは、

\begin{align}
L = \lim_{\max_{0 \leq i \leq n-1} \| P_{i+1} - P_i \| \to 0} \sum_{i=0}^{n-1} \| P_{i+1} - P_i \| \tag{2}
\end{align}

で与えられます。

ここで、極限を単純にとしていない理由は、区間の分割の方法は何通りでもあるからです（別に等分割とは一言も言っていないことに注意）。

このため、Wikipediaの定義ではを使っており*3、私は最も長い分割の長さが0になるように、としています。

厳密に理解できていなくても、折れ線で曲線を近似することで長さを求めているんだな、と思っていただければ十分です。

定理の証明

（記号の混同を避けるため、扇形の中心角をに書き換えています）

上でも言ったとおり < は認めても良いと思いますので、弧ABの長さを上から評価する部分から書いていきます。

前の節と同様に集合を定義しておきます。

このとき、以下のようにを定義すると、三角不等式より

\begin{align}
l := \sum_{i=0}^{n-1} \| P_{i+1} - P_i \| \leq \sum_{i=0}^{n-1} \left( |x_{i+1} - x_i| + |y_{i+1} - y_i| \right)
\end{align}

が得られます。ユークリッド距離とマンハッタン距離の比較と見てもいいかもしれません。

ここで、と仮定すると、この範囲では必ず < かつ > が成り立つので絶対値を外すことができ、

\begin{align}
\sum_{i=0}^{n-1} \left( |x_{i+1} - x_i| + |y_{i+1} - y_i| \right) = x_0 - x_n + y_n - y_0
\end{align}

が従います。の定義よりだったので、は線分HBの長さ、は線分HAの長さとなり、すなわち

\begin{align}
x_0 - x_n + y_n - y_0 = 1 - \cos \theta + \sin \theta
\end{align}

が分かりました。ここまでの結果を合わせると、

\begin{align}
l \leq 1 - \cos \theta + \sin \theta
\end{align}

という不等式を得ます。ここからもう少し変形します。

\begin{align}
l &\leq 1 - \cos \theta + \sin \theta \\
&\leq 1 - \cos^2 \theta + \sin \theta \\
&= \sin^2 \theta + \sin \theta \\
&= \sin \theta (\sin \theta + 1)
\end{align}

ここで、曲線の長さの定義からとすればは弧ABの長さに等しくなるので、

\begin{align}
\theta \leq \sin \theta (\sin \theta + 1)
\end{align}

が成り立つことが分かりました。

既に得られていた結果と合わせると、

\begin{align}
\sin \theta < \theta \leq \sin \theta (\sin \theta + 1)
\end{align}

となるので、より全体をで割れば、

\begin{align}
1 < \frac{\theta}{\sin \theta} \leq \sin \theta + 1
\end{align}

が得られます。

従って、とすればはさみうちの原理より

\begin{align}
\lim_{\theta \to +0} \frac{\sin \theta}{\theta} = 1
\end{align}

が示されました。（が負の場合は省略）

参考文献

takeno.iee.niit.ac.jp

*1:似た意味での誤った証明として、L'Hôpitalの定理を使ってしまうものも挙げられます。

*2:ここの詳しい内容も勉強したら別の記事にしたいと思っています。

*3:三角不等式より、分割を増やしていくことで求めたい曲線の長さに下から漸近していくことになります。

調和級数が、収束する？

調和級数は、収束しないよ。（釣りタイトルじゃん）

なんてこった……。

じゃあ、こういう級数を考えてみましょう。

とりあえず、調和級数*1と同じ級数を用意します。

\begin{align}
1 + \frac{1}{2} + \frac{1}{3} + \frac{1}{4} + \frac{1}{5} + \frac{1}{6} + \frac{1}{7} + \frac{1}{8} + \frac{1}{9} + \frac{1}{10} + \cdots
\end{align}

ここから、分母の整数を10進法で表記したときに、いずれかの桁に"9"を含むものを除きます。

つまり、 などを除いて和をとります。

この無限和はどういった値になるでしょうか？

そもそも、収束性は？

自分で考えたいという方は、ここで少し立ち止まってみてください。

実はこの級数、収束します。
具体的な値は、おおよそ23程度になります。

直感的には、大きい桁数の整数ほどその中に"9"を含んでいる可能性が高いですから、その分和が小さくなっているというわけです。

また、これは"9"ではない他の数字（あるいは任意の桁数の整数）を除いても、同様に収束します！

この級数には、Kempner級数という名前がついています。Kempnerというのは、この級数について初めて研究をした数学者の名前です。

下に"9"を除く場合の数学的な証明を載せておきます。（Wikipediaより）

証明

分母の桁数ごとに和を分割する。

桁の正整数であって、"9"を含まないものは、 個存在する。
（先頭の桁のみ"0"を選ぶことができない）

任意の 桁の正整数 に対して、 が明らかに成り立つ。よって、両辺の逆数をとることで  を得る。

ここで、全ての についての和をとれば、分母が 桁の正整数であって"9"を含まないものについての和は、 で上から抑えられる。

したがって、Kempner級数の和は高々 である。

*1:すべての正整数の逆数和

お酒と消毒用アルコールの違いって何？調べてみた！

※一部正確性に書ける部分等がある可能性があります。また、記事の内容は安全性を保証するものではありません。

ある日、友人とこのような話をしました。

「酒と消毒液の違いって何？」

いや、そりゃあ違うもんだろ……と直感的に思うのですが、じゃあ具体的に何の差異があるのかと考えると、詰まってしまいました。結局アルコールの濃度が違うんだろうな……みたいな感じで放置していたので、せっかくなので調べました。

そもそもお酒とは？

差異を語る前にそもそもの定義をしておかないといけませんから、これからやっていきましょう。

酔いのメカニズム｜人とお酒のイイ関係｜アサヒビール

こちらのサイトによりますと、日本国内ではアルコールを1%*1以上含む飲料のことをお酒としているようです。

さて、ここで注目するべきはアルコールというというところです。すこし化学を勉強している人ならば、「アルコールにも色々あるだろ」と思われるかと思います。

お酒に利用されているのは、アルコールの中でもエタノール  という物質です。そしてこれが、お酒がお酒たる所以というわけです。
エタノールには麻酔作用があり、これがいわゆる「酔い」の原因となります。

また、同じアルコールにメタノール という物質があります。
こちらは同じアルコールという部類でありながら、人体に有害であり飲料に用いることはできません。これは代謝の過程でメタノールの酸化によって生じるホルムアルデヒド やギ酸 の影響とされています。

消毒用アルコールの成分は？

同様に、消毒用アルコールについても見ておきましょう。
こちらもさっきからずっとアルコールと言っていますが、主成分はエタノールです。

エタノールですが、実は市販されているものはだいたい次の2つに分かれています。ついでなので、ここで触れておきます。

無水エタノール（99.5 vol%以上程度）

無水エタノールは、水分をほとんど含まない純度の高いエタノールです。

「純度が高いならばこれを消毒に使えばいいのではないか？」と思うかもしれませんが、実はこの無水エタノール、純度が高すぎるがゆえにすぐ揮発してしまい、その場に残留しないので、一般に想像されるような消毒作業には逆に向いていません。

この性質から、水拭きできない電気製品の洗浄などに使われるそうです。

ところで、エタノールと名前は付きますが、実は無水エタノールは飲んではいけません。なぜでしょうか？

濃度に注目してみましょう。99.5%です。これを達成するためには、どういった作業が必要でしょう。

当然、何度も蒸留をして無水エタノールは生成されています。
しかしながら、エタノールと水の混合物を単に蒸留しても、実は95%以上の濃縮ができません。これは化学的な理由からだそうですが、私自身詳しくないので、みなさん自身に調べてもらいたいと思います。

ともかく、このままでは99.5%を達成できませんから、どうするかというと、混合物にベンゼンを加えて蒸留します。こうすることで、無水エタノールを精製することができます。

このベンゼンというやつは、発がん性があったりする危険な物質です。飲むのは当然よくないですし、吸引もあまり好ましくないでしょう。
こういった物質が無水エタノールには残留している可能性があるので、希釈したとしても飲むことはできません。

消毒用エタノール（75 - 80 vol%程度）

こちらが今回取り扱うエタノールです。

無水エタノールよりも濃度が下げられており、名前の通り消毒に適しています。私達が普段一番見る機会が多いのは、この消毒用エタノールでしょう。

これを果たして飲むことは可能なのか？この疑問は次の節で扱うことにします。

先に述べておくべき注意として、この消毒用エタノールにはそもそも飲むことができない亜種があったりします。そのうちの1つが、2-プロパノール  が添加されている消毒液です。

2-プロパノールもアルコールの一種ですが、少し毒性が強く内服等はしていけない物質です。
なぜこれを消毒液に添加するのか。

理由は、酒税を回避するためです。

「えっ、酒税？」

はい、実は飲むためのものとして売られていない消毒用エタノールにも、酒税の分価格が上乗せされています。それは飲めるということでは？

これを回避して価格を下げるために、メーカーによってはこういった対処をして「お酒」のグループに属さないようにしていたりします。

結局、お酒と消毒用エタノールの違いとは？

結論から言うと、本当に濃度くらいしか差がなさそう。

いや、まあ当然お酒には穀物みたいなのが含まれていたりしますし、アルコールだけとか味ねえじゃんみたいな話はありますが、主成分のエタノールについてだけ見れば、濃度が違うだけの水溶液だと思えばいいでしょう（適当）。

もしアルコール中毒でどうしてもアルコールを摂取したい場合には、消毒用エタノールを精製水で割って飲めば、いいんじゃないかな。当然責任は一切負いませんが。

消毒液はさっき言ったように添加物で界面活性剤等が入っていたりするのもありますから、それだけ注意しましょう。

*1:おそらくvol%（体積パーセント濃度）だと思われます。

導出: Riemannゼータ関数の特殊値のBernoulli数による表現

書いておきたい数学の話があったので、書きます。
タイトルの通りです。

sin xの因数分解

今回の話は、以下の式から始まります。

\begin{align}
\sin (\pi x) = \pi x \prod_{n=1}^{\infty} \left( 1 - \frac{x^2}{n^2} \right)
\end{align}

は任意の実数とします。（この等式自体は、複素数に拡張しても成立します）

形式的には、正弦関数を因数分解した式となっています。
高校数学では多項式関数に対して因数定理というものがありましたが、これは少し条件を加えることで一般の複素数値整関数にも同様の議論が適応できて、しかも零点が無限個でも許容されます。（Weierstrassの因数分解定理）

ここで、両辺の自然対数（主値）を取ります。

\begin{align}
\log \sin (\pi x) = \log \pi x + \sum_{n=1}^{\infty} \log \left( 1 - \frac{x^2}{n^2} \right)
\end{align}

さらにこれを両辺 で微分します。
すると、両辺はそれぞれ次のようになると思います。

\begin{align}
\pi \frac{\cos (\pi x)}{\sin (\pi x)} = \frac{1}{x} - 2 \sum_{n=1}^{\infty} \frac{\frac{x}{n^2}}{1 - \frac{x^2}{n^2}}
\end{align}

両辺に をかけて整理します。

\begin{align}
\pi x \frac{\cos (\pi x)}{\sin (\pi x)} = 1 - 2 \sum_{n=1}^{\infty} \frac{\frac{x^2}{n^2}}{1 - \frac{x^2}{n^2}} \tag{1}
\end{align}

さて、ここで左辺と右辺についてそれぞれ考えていきましょう。

左辺を級数に変形する

\begin{align}
\pi x \frac{\cos (\pi x)}{\sin (\pi x)}
\end{align}

左辺は上のような形になりましたが、これは複素指数関数（Eulerの公式）を用いて書き直すことができるでしょう。

\begin{align}
\pi x \frac{\cos (\pi x)}{\sin (\pi x)} &= i \pi x \cdot \frac{e^{i \pi x} + e^{- i \pi x}}{e^{i \pi x} - e^{- i \pi x}} \\
&= i \pi x \cdot \frac{e^{i \pi x} - e^{- i \pi x} + 2 e^{- i \pi x}}{e^{i \pi x} - e^{- i \pi x}} \\
&= i \pi x \left( 1 + \frac{2 e^{- i \pi x}}{e^{i \pi x} - e^{- i \pi x}} \right) \\
&= i \pi x \left( 1 + \frac{2}{e^{2 i \pi x} - 1} \right) \\
&= i \pi x + \frac{2 i \pi x}{e^{2 i \pi x} - 1} \tag{2}
\end{align}

(1)と(2)を合わせることで、以下を得ます。

\begin{align}
i \pi x + \frac{2 i \pi x}{e^{2 i \pi x} - 1} = 1 - 2 \sum_{n=1}^{\infty} \frac{\frac{x^2}{n^2}}{1 - \frac{x^2}{n^2}} \tag{3}
\end{align}

ここで、左辺の第二項の関数を級数に展開したいと思います。

関数 t / (e^t - 1)

そのまま扱うのは面倒そうなので、 として単純化しておきます。
そうすれば、以下の関数を考えればよいでしょう。

\begin{align}
\frac{t}{e^{t} - 1}
\end{align}

これは以下のような関数と等価ですので、複素数平面全体で正則です。
（ は原点において1位の極を持ちますが、1次関数によって打ち消されています）

\begin{align}
\frac{t}{e^{t} - 1} = \frac{t}{2} \left( \coth \frac{t}{2} - 1 \right)
\end{align}

さて、この関数をそのまま微分していってTaylor級数の係数を決定していくのはかなり大変そうです。
ここで、正則という条件を使って以下のように表現できると仮定します。

\begin{align}
\frac{t}{e^{t} - 1} = \sum_{n=0}^{\infty} \frac{B_n}{n!} t^n
\end{align}

が決定できれば、Taylor展開ができたということになります。

さらに、左辺の分母も級数表現に直します。

\begin{align}
\frac{t}{\sum_{n=0}^{\infty} \frac{1}{n!} t^n - 1} &= \sum_{n=0}^{\infty} \frac{B_n}{n!} t^n \\
\frac{t}{\sum_{n=1}^{\infty} \frac{1}{n!} t^n} &= \sum_{n=0}^{\infty} \frac{B_n}{n!} t^n
\end{align}

最後に分母をはらえば、以下のようになります。

\begin{align}
t &= \left( \sum_{n=0}^{\infty} \frac{B_n}{n!} t^n \right) \left( \sum_{n=1}^{\infty} \frac{1}{n!} t^n \right) \\
&= \left( B_0 + B_1 t + \frac{B_2}{2!} t^2 + \cdots \right) \left( t + \frac{1}{2!} t^2 + \cdots \right) \\
&= B_0 t + \left( \frac{B_0}{2!} + B_1 \right) t^2 + \cdots
\end{align}

あとは、両辺で係数比較すれば係数 が決定できます。
低次の項から計算していくことで、上手く全ての係数が計算できるようになっています。

\begin{align}
B_0 &= 1 \\
B_1 &= - \frac{1}{2} \\
B_2 &= \frac{1}{6} \\
B_3 &= \cdots
\end{align}

実はこの数列には名前が付いていて、Bernoulli数と一般に呼ばれています。

Bernoulli number - Wikipedia

これを用いて、(3)は次のように書き換えられます。

\begin{align}
i \pi x + \sum_{n=0}^{\infty} \frac{B_n}{n!} (2 i \pi x)^n = 1 - 2 \sum_{n=1}^{\infty} \frac{\frac{x^2}{n^2}}{1 - \frac{x^2}{n^2}} \tag{4}
\end{align}

ゴールに近づいてきました。
次は右辺について考えていきましょう。

右辺の分解

\begin{align}
1 - 2 \sum_{n=1}^{\infty} \frac{\frac{x^2}{n^2}}{1 - \frac{x^2}{n^2}}
\end{align}

ここで被加数に注目してみると、等比級数の和の形になっていることに気が付きます。

\begin{align}
1 - 2 \sum_{n=1}^{\infty} \frac{\frac{x^2}{n^2}}{1 - \frac{x^2}{n^2}} = 1 - 2 \sum_{n=1}^{\infty} \sum_{m=1}^{\infty} \left( \frac{x}{n} \right)^{2m}
\end{align}

ここで和の順序を交換します。

\begin{align}
1 - 2 \sum_{n=1}^{\infty} \sum_{m=1}^{\infty} \left( \frac{x}{n} \right)^{2m} &= 1 - 2 \sum_{m=1}^{\infty} \left( \sum_{n=1}^{\infty} \frac{1}{n^{2m}} \right) x^{2m} \\
&= 1 - 2 \sum_{m=1}^{\infty} \zeta(2m) x^{2m} \tag{5}
\end{align}

ゼータ関数が係数に現れました。

(5)の結果を(4)に代入すれば、以下を得ます。

\begin{align}
i \pi x + \sum_{n=0}^{\infty} \frac{B_n}{n!} (2 i \pi x)^n = 1 - 2 \sum_{m=1}^{\infty} \zeta(2m) x^{2m} \tag{6}
\end{align}

係数比較

\begin{align}
i \pi x + \sum_{n=0}^{\infty} \frac{B_n}{n!} (2 i \pi x)^n = 1 - 2 \sum_{m=1}^{\infty} \zeta(2m) x^{2m} \tag{6}
\end{align}

さて、ここまでの計算で上記の結果が得られました。

注意してみると、右辺には偶数次の項しか存在しないので、このことから任意の奇数 に対して となることが導かれます。
これは奇数に対するゼータ関数の特殊値の簡易な表示が得られていないことの一因ともなっています。

一方(6)から、ある偶数 に対して は以下のように表現できることが従います。（ゼータ関数の一種の母関数が得られたとも言えます）

\begin{align}
\zeta(2m) = - \frac{B_{2m}}{2 \cdot (2 m)!} (2 i \pi)^{2m} \tag{7}
\end{align}

奇数に対する表示は未だ複雑なものしか発見されていません。

もし新しい式を発見された方がいらしましたら、ご一報ください。

RTX3070（搭載PC）を買ったので色々紹介とか

たまには普通のブログっぽいことも書こうかな～と思ったので、まず新PCについての話を書こうかなと。

TL;DR;
・RTX 3070とRyzen 7 3700XでBTO組んだよ
・自分のやるゲームだと性能持て余し気味

RTX 3000シリーズが来た！

2020年の9月2日、NVIDIAが新世代のRTX 3000(Ampere)シリーズを発表しました。最上位モデルのRTX 3090をはじめ、3080・3070も「FASTER THAN 2080 Ti」ということらしい……（3070は2070 SUPERの後継のはずでは…）。1080 Tiすげえと言っていた時代がもはや懐かしい。値段的にも、RTX 3070はRTX 2080 Tiの半額以下でこのスペック。

www.nvidia.com

このときは全くパソコン買い換える予定もなかったので、本当に「すげえな～～」という気持ちでしか見ていなかったのですが、10月中頃になって諸事情により予算があるやんということになり、このタイミングでパソコンを買い換えようということになりました。ナイスタイミング。

ちなみに旧PCのスペックは、CPUがIntelのCore i7-6700HQ、グラフィックカードがGeForce GTX 960M、RAMが16GBという感じでした。パーツからも分かる通りゲーミングノートPC（G-Tuneさんのところで買いました）で、3年ほど前に買ったものです。

予算もかなり絞った上での初めてのゲーミングPCだったので、まあこんな感じです。
最初はMinecraftくらいしかやる予定が無かったので、このスペックで特に困ってもいなかったのですが、最近になってFPS等々3Dゲームをやることが増えてきて、実際にApexをプレイしてても支障があるくらいの性能だったので、長らく買い替えたいな～と思っていました。

そして新PCへ…

3090と3080は9月中にすでに販売開始されていたものの、流石にお高いなあという気持ちがあったので、10月末の3070の発売を待ってから色々BTOメーカーを見比べて買うことにしました。前が960Mなのでこの時点でベンチのスコア10倍くらいあるんですよね……。

その後、発売日の10月29日に有名どころのBTOメーカーさんのサイトを見に行くとパソコン工房さんとドスパラさんが早速3070搭載のものを出していて、G-Tuneさんは3090と3080のものしかまだ出てないという状況だったので、簡単に比較して今回はパソコン工房さんで買うことにしました。

自分がそこまでPCパーツもメーカーさんも詳しいわけじゃなかったので雰囲気で決めたのですが、BTOだとFRONTIERさんがコスパとても良いらしいですね。これから買いたい人には結構おすすめです。FRONTIERさんも歴史の長いメーカーさんなので、安心。

www.frontier-direct.jp

今回買ったパソコンが、こちら。

www.pc-koubou.jp

カスタマイズですが、ほとんど弄ってません。
個人的にOS用のSSDとゲーム用のSSDを別にしたかったので、これだけ分けました。

メインSSDをなんとなくM.2に

物置用のHDDは元々2TBだったのでそのまま。

全部合わせて、パソコン本体は税別181,940円という感じです。税込みでぴったり20万くらいですね。

ほとんどの人が満足できるスペックだと思うので、これが20万というのは凄いなあと思います。

パソコン工房さんでBTOパソコンを買うときの注意（？）

パソコン工房さんでパソコンを購入すると、他の通販サイトと同様に翌日くらいに注文確認のメールが届きます。この中に発送予定日という項目があります。

確認しておきましょう

ここでは「1～2週間」となっていますが、パソコン工房の公式サイトのQ&Aのところにもある通り、通常最大日数で出荷されるようです。
（私の場合もメールが届いてから14日目に発送の通知がありました）

なかなか発送されなくても仕様です

これは去年のQ&Aですが、今でも同様になっているようです。

ついでに色々買った

パソコンを買い替えたのはいいものの、今まではずっとWindows XP時代から10年近くノートPCだったのでまずキーボードとディスプレイを初めて買いました。

最近ずっとApexをやってるのもあって、ディスプレイは144Hzとかリフレッシュレート高めのやつに憧れがあったので、これを買ってみました。

1　6　5　H　z

これはAmazonで25800円で購入。ゲーミングモニターってもっと高そうだと思っていたので結構助かりました。ASUSありがとう。

あとはキーボード等々。

Logicool信者

正確な値段は忘れてしまいましたが、3つ合わせて20000円もしないくらいです。（秋葉原のヨドバシ価格）

ゲーミングデバイス買うのも初めてでこだわりも特に無かったので、スタンダードなものを一式買ってみました。G203とかはエントリーモデルという感じですね。

デスクトップPC初心者の失敗

ディスプレイとパソコンを繋げようとしたときに一生マザーボードのDisplayPortの穴にケーブルを刺していて「ディスプレイに出力されないんだが？」状態になってました。

ちゃんとグラフィックボードの端子に刺しましょう。

ベンチとかその他

ベンチマークとかやりたいので、これはまた別の記事にでもしようかなと思っています。

パソコンを買い替えてみた総評ですが、とりあえず前々からあったRyzen使ってみたいなという夢とかRTX買ってみたいという夢が叶ったので個人的には大満足です。

全部合わせて24万くらいなので決して安い買い物ではなかったですが、値段以上のリターンを得られていると感じます。まあ、3070を活かしきれているかというとまだ微妙なのですが……。

3DCGとかも触りたいのでこれから頑張ってくれるでしょう。

ゲーミング環境を変えて一週間後のApex

初3000ハンマー（レイス使い始めて1週間目）

結論：環境は整えたほうが良い。

Minecraftで学ぶJavaプログラミング入門 #2: アイテムの追加

MinecraftのMod開発講座、第2回です。

mikan-alpha.hatenablog.com

前回は、開発を始まるまでの下準備を行いました。
今回から実際にゲームに触れてみましょう。

1. プロジェクトのインポート

Eclipseを起動します。

ロードの途中で、ワークスペースを選択するウィンドウが出ますので、適当なディレクトリをワークスペースにしておきます。
私はMod開発用に新規でディレクトリを作成してそれを選択しました。

ロードが完了したら、エディターが開きます。

初期状態

ここで、前回用意したプロジェクトを開きます。

メニューのファイルから、インポートを選択します。
ここで、「既存のGradleプロジェクト」を選びます。

検索すると、はやい！

次の画面で、前回用意したForgeのディレクトリを指定します。

あとは、完了を押して待ちます。

インポートが完了したあと、こんな感じで色々ずらっと増えていたらOKです。

読み込み後

試しに、src/main/javaの中の、com.example.examplemodパッケージに入っているEampleMod.javaを開いてみます。

Javaの世界へようこそ

こんな風に中身が問題なく表示できれば良いです。

ここから、開発を始めていきましょう。

2. Javaの基礎の話

一応Javaに触れたことない人にも読んでもらうことを目指しているので、今回出てくる要素の解説をざっくりと。

プログラムの書き方

Javaにおいては、セミコロン（;）で処理のまとまりを区切ってプログラムを書いていきます。基本的には、行の先頭からその行のセミコロンまでを処理のひとまとまり（最小単位）だと思っておけば問題ないでしょう。
このセミコロンの前に記述してある内容が、コンピューターへの命令となるわけです。

この処理がいくつか集まって、{}で囲まれたブロックのことを、Javaではメソッド（関数）と呼びます。細胞の集合が組織みたいなものです。
関数と書いたとおり、数学の経験がある人は数学の関数と同じと思ってもらって構いません。
何か入力を受け取って、中でなんらかの処理をして、そして値を返します*1。

上で見たソースコードには、たくさん関数が記述されています。

先頭に修飾子、返り値の型(void)、メソッド名、引数の情報があり、{}で囲まれている範囲がこのメソッドの処理内容です。修飾子については詳しくは触れませんが、どこからこのメソッドにアクセスができるか、などのような情報を表すタグのようなものです。

さらにこのメソッドがいくつか集まってできるのが、クラスです。
Javaでプログラミングをしていく際の基本単位です。

先程のソースコードでは一番外側にこのように書かれています。

メソッドと同様に、修飾子が付いていてその後にclass、そしてクラス名となっていて、{}で囲んだブロックがこのクラスになります。

変数（メンバ変数、ローカル変数）

プログラミングに欠かせない要素の1つが、変数です。

これも、数学の変数と同じものと思ってもらっていいでしょう。

ただ一つ違う点があるとすれば、変数の中身が「数字」とは限らない、という点です。

例えば、「hello」という文字列を変数に代入することもできるし、何かオリジナルのオブジェクトを代入することもできます。このあたりは、この後すぐ出会うことになります。

こんな風に変数に色んなものを入れておけるので、中に何が入ってるのかコンピューターに教えるために、変数には「型」という概念があります。

変数を宣言したいときには、「型名 変数名;」というように記述します。

例えば、「int x;」と書くと(32bit)整数型の変数が一つ確保されます。
上の例で出した文字列の変数を宣言したければ、「String str;」というように。
変数名は、1文字でなくても良いです。というより、むしろプログラミングにおいては分かりやすい名前にしておくべきでしょう*2。

上で見たソースコードにおいては、例えばこれが変数です。

変数の例

先頭の紫文字は今は無視して、型名と変数名を見ましょう。
この変数の型は「Logger」で、変数名は「LOGGER」ということになります。

またこの例のように、宣言と同時に変数に何か代入しておくこともできます。
Javaにおいては、「=」は（右辺を左辺に）代入の意味になりますので、プログラミングを始めたばかりの人は注意すべきポイントです。

また、変数には2種類あって、メンバ変数とローカル変数というものがあります。

この先で出てくる内容を含みますが、一応説明をしておくと、メンバ変数はクラス内かつメソッド外で宣言される変数、ローカル変数はメソッド内で宣言される変数という定義です。メンバ変数は、クラス内のメソッドだけでなくクラス外からも参照できたりしますが、ローカル変数は宣言されたそのメソッド内からのみ参照できる変数となります。（変数のスコープ）

3. Modをゲームに認識させる

先程開いたExampleMod.javaをそのまま書き換えていっても良いのですが、一応パッケージだけ作り直しておきます。

Javaの一般的な命名規則に従いました

ここで、これから作るModのIDを決めます。ユニークな文字列である必要があります。他のModと被らないものにしましょう。

決めたら、IDと同じ名前のパッケージを作ってそこにExampleMod.javaをコピーしておきます。

IDは「tutmod」にしました

リネームもしておきました。元々あったパッケージは削除して構いません。

さて、このプログラムをゲームに認識させるために、少しだけやることがあります。

まずこのクラスに付いているアノテーションの値を、先程自分で決めたIDに書き換えます。

次に、mods.tomlを開きます。

開いたら、modId=のところの値も自分のIDに書き換えます。

必要に応じて、他のところも書き換えておきましょう。
ここではdisplayName（表示名）だけ変えておきました。

他にもModのロゴ画像を表示できたり、公式サイトを載せたりできるので、確認してみてください。

最後に、メニューの「プロジェクト」からプロパティを開きます。

実行/デバッグ設定を開くと、以下のように予め3種類の起動構成が用意されているはずです。

ここで、「runClient」と「runServer」とそれぞれ編集します。

「環境」タブを開いて、MOD_CLASSESの「examplemod」と書いてある部分を自分のIDに置換してください。

終わったら、適用を押して閉じます。

準備が終わったので、この状態でデバッグをしてみましょう！

今編集した「runClient」を実行してみます。

こんな感じにMinecraftが起動できれば問題なしです。

Modsを開いて、今開発しているModが読み込まれていることを確認します。

lorem ipsumが読めます。

4. 無機能アイテムを追加する

Modを開発する準備も完璧に整いました。
ここから実際にアイテムを作ってみましょう。

アイテム本体

まずはアイテム本体のクラスを準備します。
管理のためにitemというパッケージを新しく作成して、そこにアイテムのクラスを入れていくことにします。

クラス名はMinecraft本体の命名規則に従っています

クラスを新規作成すると、最低限の記述のみのソースが自動で生成されます。

ここで、Minecraft本体のItem（net.minecraft.item.Item）クラスを継承します。

Eclipseの機能でコンストラクタも簡単に生成してくれます

こうするだけで、Minecraftのアイテムの最小限の機能だけを持ったアイテムが作れます！

右クリックしたときの処理を追加するとか、そういった独自の機能を持たせたい場合にはこのクラスでItemクラスのメソッドをオーバーライドしていきます。

アイテムの基本の設定だけしましょう。

コンストラクタにあるProperties（Item.Properties）の設定をします。これは名前の通りで、アイテムが最大で何個スタックできるか、耐久値はいくつか、どのクリエイティブタブに属するか、のような情報を持つクラスです。

今は飛ばしてしまうので、インスタンスだけスーパークラスに投げておきます。

次の行で、このアイテムのシステム内名称を設定しています。これは必ず設定しなければなりません。setRegistryNameの第1引数はMODのId、第2引数にアイテムの名前を渡します。

メインクラスでMODのIdを管理するようにしました

これで、アイテム自体は完成です。

アイテム登録用クラス

次にこのアイテムをゲームに登録します。
ModItemsというクラスを作って、そこでアイテムのインスタンス管理をすることにします。

こんな感じにアイテムを入れる変数とメソッドを定義してあげて、ゲームの初期化時にこのinit()を呼んであげればよいです。

publicにするのを忘れずに

外からアクセスするものなので、publicにします。

ゲーム初期化時にアイテムを登録する

Modのメインクラスに戻ります。下の方にいくと、RegistryEventsというクラスがあると思います。

ここにブロック登録用のメソッドが予め書かれているので、これを真似してアイテム用のメソッドを作ります。

ここでアイテムやブロックを登録します

onItemsRegistryの中で、ModItems.init()を呼び出して、そしてアイテムを登録します。

初期化を忘れるとぬるぽになる

これでゲームにアイテムが追加できたので、Minecraftを起動してみます。

giveコマンドでアイテムを召喚するとこんな風になると思います。

視界の1/4が謎の物体で埋まります。

ここから、テクスチャやアイテム名のローカライズの設定をしましょう。

5. アイテム名などを設定する

アイテム名などの設定は、あまりプログラムを使わずにできます。

src/main/javaではなくて、src/main/resourcesの方を開いて、以下のようにパッケージを作ります。
リソースパックなどに触れたことがある人は馴染みがあると思いますが、assetsの後ろがminecraftではなくてModのIdになるので気をつけましょう。

リソースパックと同じ

アイテム名を設定する

アイテム名のローカライズは、JSONを利用します。

以下のように、例として英語用の言語ファイルを作ってみます。

日本語ならja_jp.json

記法はJSONそのままです。左側にローカライズ前の文字列、右側にローカライズ後の文字列を書けばあとは勝手にゲーム側で書き換えてくれます。

アイテム名以外のローカライズにも使います。書き方は全部同じです。

このようにちゃんとローカライズされていたらOKです。

テクスチャを設定する

テクスチャの設定もJSONです。models.itemの中にアイテムのRegistryNameと同じ名前のファイルを置いておくだけで勝手に読み込んでくれます。

コピペ

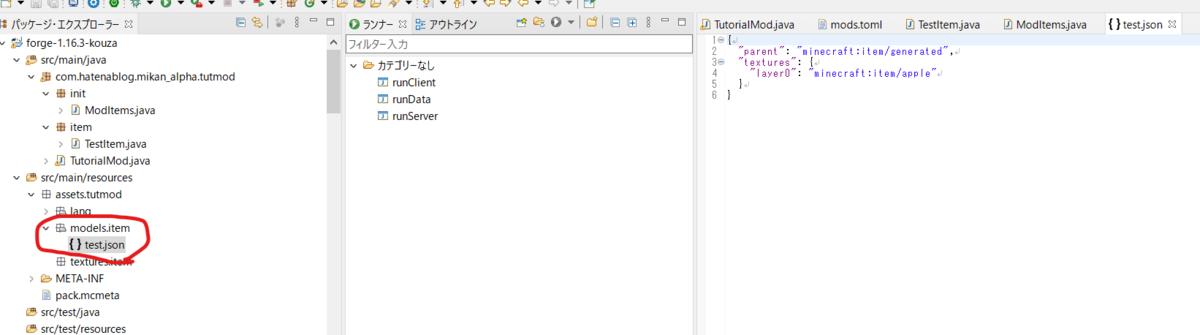
ファイルの中身はバニラのリンゴからコピペしました。

自作のテクスチャにしたい場合には、layer0の値を書き換えます。

できた

6. 次回予告

今回はアイテムをやったので、次回はブロックの追加をします。

実は、結構似ているので次回は楽かもしれません。その後はレシピかな？

それではまた次回。

*1:ただし入力を受け取らない関数や値を返さない関数もあります

*2:変数名の長さは重要度に比例し、使用頻度に反比例すると良いです。

Minecraftで学ぶJavaプログラミング入門 #1: 開発環境の準備

※この講座は、以下のバージョンを想定しています。
Minecraft JavaEdition (1.13.x-)1.16.x
Minecraft Forge 34.1.0 (for 1.16.3)

1. はじめに

お久しぶりです。元々はYouTube上で動画にでもしようかと思っていたのですが、個人的に撮影する時間があんまり取れなさそうだったので、とりあえず文字ベースでやってみようかと思います。よろしくお願いします。

想定している読者は、（PCの）Minecraftをプレイしたことがあって（これが大事）、プログラミングはやったことないけど興味がある*1とか、ゲーム開発楽しそうだけど敷居が高くてあんまりできてないとか、そういう人たちです。

1からゲームを作るのとはまた違いますが、なんとなくゲームプログラミングの楽しさが伝わるといいなと思います。書いてる人がそもそもプログラミング素人なので、そんな高度なことはしません。というより、できません。気軽に読んでもらってOKです！あとはパソコンの基本的な操作とかができれば可。

この講座の目的は、MinecraftのModを自分の手で作りながら、Javaの基礎に触れることです。プログラミングをしなくてもModが作れるツールみたいなのもあった気がしますが、やっぱり自由度は格段に違いますし、何よりコードを書いてると頭がよくなった気分になれて楽しい！！！！ので、ここでは自分でコーディングします。

以下、目次です。

2. Java(JDK)をインストールする

さて、早速始めていきましょう。

Minecraftというゲームは、上でも少し話した通り、Javaという言語で書かれています。なので、基本そのModもJavaを用いて作ることになります*2。

Minecraftというゲームは便利にできていて、ただプレイするだけならランチャーが勝手にJavaの実行環境(JRE)を用意してくれます。つまり、パソコンにわざわざJavaをインストールする、ということをせずに遊べてしまうわけです。

ただこの実行環境というのはランチャー内で使うだけの専用のものになっていて、「Javaでプログラミングしたい！」となったときは別途準備する必要があります。
（既にJDKを使ったことがある人はこの項は飛ばして構いません）

ここで登場するのが、JDK改めJava Development Kitです。

これは、Javaでプログラミングをするために必要な道具が一式そろった開発キットです。Mod開発をしていくにはこれがないと始まりせんので、準備しましょう。

本講座ではAmazonさんのAmazon Corretto 8を使うことにします。

aws.amazon.com

上のページからAmazon Corretto 8をダウンロードして、インストールしてください。

ボタンを押すとダウンロードURLがずらっと出てくるので、お使いのプラットフォームに合わせたものをダウンロードしましょう。

Windowsの場合は、インストーラー形式(.msi)のものが一番簡単だと思います。

2. 統合開発環境(IDE)を用意する

さて、プログラミングに欠かせないものと言えば、便利なエディタです。ここでは、Minecraft Forgeも標準でサポートしている、Eclipseというエディタを使います。

Google等で「Eclipse」と検索すると以下のサイトがトップに出てくると思います。

mergedoc.osdn.jp

サイトトップのページから「Eclipse 2020」を選択します。

移ったページで、Javaの欄のFull Editionから同様にお使いのプラットフォームのEclipseをダウンロードします。

サイズが大きいので、気長に待ちましょう。

（あれ、JDK自分で用意する必要なかったな……？）

ダウンロードが終わったら、インストールする必要はないソフトなので解凍して分かりやすい場所に置いておいてください。

3. Minecraft Forgeのセットアップ

ここからは、MinecraftのMod開発特有の準備です。

今回はMinecraft Forgeを使ってModを作るので、この下準備をします。

Google等で「Minecraft Forge」で検索すると公式サイトがヒットします。

files.minecraftforge.net

現在(2020/11/08)はトップにMinecraft 1.16.3用のものが表示されていますが、そうでなければ左のメニューから1.16.3を選択してください。また、異なるバージョンのModが作りたい場合には同様に左メニューからModを作りたいバージョンを選びます。
（この講座で扱うバージョンでない場合、Modの書き方が大きく異る場合があるのでそれぞれのバージョンの講座を参照してください）

バージョンを選択したら、Recommended（推奨版、安定版）の方のMdkをダウンロードします。

Sourcesではないので注意（昔はMdkがsrcでした）

別にLatest（最新版）でもいいのですが、Recommendedがある場合はこちらを選んでおいた方が無難です。Forgeに滅多にバグは見ないのですが*3、念の為。

これもダウンロードが済んだら解凍して分かりやすい場所に置いてください。
解凍する場所ですが、パスに2バイト文字が含まれない場所が望ましいです。

次に、これをこれから使うためのセットアップをします。

「gradlew」等があるトップの階層に、バッチファイルを作成します（Windowsの場合）。

setup.batという名前で作成しました

そしてこのバッチファイルの中身に、「gradlew genEclipseRuns」と書いて起動します。

※表示される内容は若干異なっていて大丈夫です

これも時間がかかりますので、お茶でも飲みながら気長に待ちます。
特にエラー等吐いてなければ問題ないです。

最後に緑文字が出てプロンプトが閉じたら準備完了です！お疲れさまでした。

ディレクトリ内に色々ファイルが増えていると思います。

4. 次回予告

今回でMod開発を始めるための準備が整いました！

次回は実際に、無機能なアイテムをゲームに追加してみたいと思います。

今回はまだコーディングする場面がありませんでしたが、次回からは逆にほぼずっとコーディングです、お楽しみに。

*1:でも、入門とは書いたけど本当にやったことないとちょっと難しいかも……。C++みたいな似た言語を触ったことがあれば、とても役に立つと思います。

*2:Kotlinでもできたりしますが、ここでは触れないことにします。

*3:自分も過去一度しかForge自体が原因のバグに遭遇したことがないです。