座標平面上の三角形の面積公式

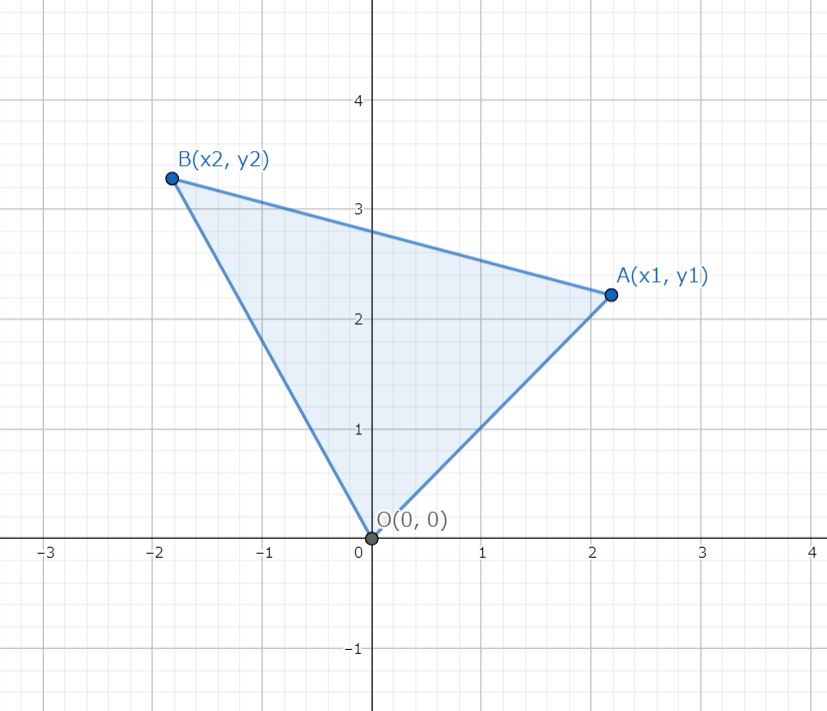
定理. 座標平面上の原点、2点とが一直線上にないとき、この3点を頂点とする三角形の面積は以下の式で表される。

\begin{align}
S = \frac{1}{2} | x_1 y_2 - x_2 y_1 |
\end{align}

証明

を 、 を 、 を と置く。

\begin{align}
S &= \frac{1}{2} \| \vec{a} \| \| \vec{b} \| \sin \theta \\
&= \frac{1}{2} \| \vec{a} \| \| \vec{b} \| \sqrt{1 - \cos ^2 \theta} \\
&= \frac{1}{2} \sqrt{\| \vec{a} \| ^2 \| \vec{b} \| ^2 (1 - \cos ^2 \theta)} \\
&= \frac{1}{2} \sqrt{\| \vec{a} \| ^2 \| \vec{b} \| ^2 - \| \vec{a} \| ^2 \| \vec{b} \| ^2 \cos ^2 \theta} \\
&= \frac{1}{2} \sqrt{\| \vec{a} \| ^2 \| \vec{b} \| ^2 - (\vec{a} \cdot \vec{b}) ^2} \\
&= \frac{1}{2} \sqrt{(x_1^2 + y_1^2) (x_2^2 + y_2^2) - (x_1 x_2 + y_1 y_2) ^2} \\
&= \frac{1}{2} \sqrt{(x_1^2 + y_1^2) (x_2^2 + y_2^2) - (x_1^2 x_2^2 + y_1^2 y_2^2 + 2 x_1 x_2 y_1 y_2)} \\
&= \frac{1}{2} \sqrt{x_1^2 y_2^2 - 2 x_1 x_2 y_1 y_2 + x_2^2 y_1^2} \\
&= \frac{1}{2} \sqrt{(x_1 y_2 - x_2 y_1) ^2} \\
&= \frac{1}{2} | x_1 y_2 - x_2 y_1 |
\end{align}